Теория кристаллического поля (ТКП) — теория, созданная для описания и предсказания некоторых физических и химических свойств комплексных соединений, которая фактически является развитием простой модели электростатического взаимодействия при образовании комплексов.
Теория кристаллического поля основана на главном предположении, что каждый лиганд L представляет собой точечный заряд (отрицательный), который не обладает ни формой, ни размерами, ни особенностями химической природы.
В ТКП рассматривается взаимодействие данных лигандов — точечных зарядов — с d-орбиталями металлов, пространственное расположение которых учитывается в рамках теории.
Применение теории
Началом описания строения комплексов в ТКП служит рассмотрение взаимодействия лигандов (точечных зарядов) с d-орбиталями центрального иона. Чаще всего теория кристаллического поля и её основные понятия рассматриваются на примере октаэдрических комплексов — наиболее распространённых в координационной химии.
Октаэдрические комплексы. Общие понятия
Для удобства рассмотрения вводится трёхмерная декартова система координат, в которой по осям \(x, y, z\) располагаются лиганды, образующие октаэдрическое окружение. На рисунке ниже они обозначены красными точками:

Лиганды несут в себе отрицательный заряд, также как и d-орбитали металла. Это означает, что чем ближе находятся лиганды и орбитали, тем сильнее становится их взаимодействие, и за счёт одинакового знака заряда по закону Кулона происходит отталкивание и, следовательно, повышается энергия орбиталей.
Две из пяти d-орбиталей — \(d_{z^2}\) и \(d_{x^2-y^2}\) — вследствие своей формы оказываются ближе к лигандам, так как они направлены вдоль координатных осей \(x, y, z\). Следовательно, данные орбитали приобретают бо́льшую энергию, чем остальные три (см. далее).

В свою очередь, оставшиеся 3 орбитали \(d_{xy}, d_{xz}, d_{yz}\) расположены так, что их «лопасти» находятся между координатными осями. Это делает их более удалёнными от лигандов (и менее направленными к ним), и обеспечивает меньшее взаимодействие с ними по сравнению с орбиталями \(d_{z^2}\) и \(d_{x^2-y^2}\):

Вследствие вышеперечисленных эффектов орбитали, изначально (в отсутствие лигандов) имевшие одинаковую энергию, «расходятся» по энергии на определённую величину, называемую энергией расщепления кристаллическим полем, и обозначаемой как дельта-октаэдрическое \(\Delta_o\) (для октаэдрического расщепления). Также встречается обозначение \(10 Dq\).

Орбитали, находящиеся ниже по энергии, становятся выгоднее для заполнения электронами. Их «выигрыш» (разница) в энергии относительно начального уровня d-орбиталей составляет \(\frac{2}{5}\Delta_o \), а, в свою очередь, «проигрыш» в энергии ставших невыгодными орбиталей \(d_{z^2}\) и \(d_{x^2-y^2}\) составляет \(\frac{3}{5}\Delta_o\):
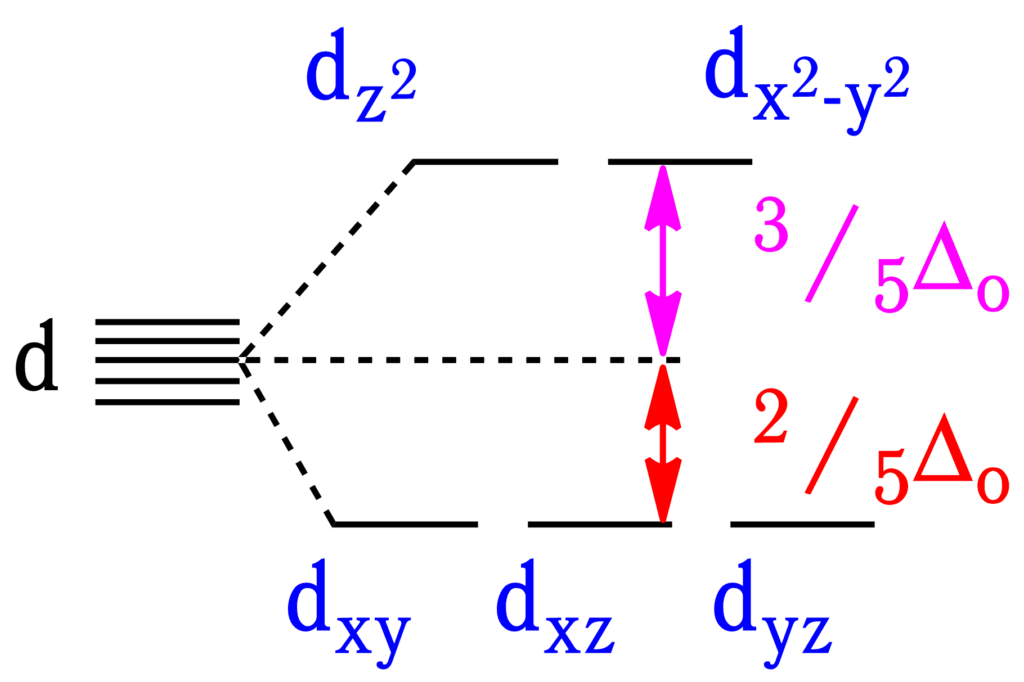
Орбитали, находящиеся выше по энергии, имеют симметрию \(e_g\) — дважды вырожденные, симметричные относительно центра инверсии; в свою очередь лежащие ниже по энергии орбитали имеют \(t_{2g}\)-симметрию (трижды вырожденные, симметричные относительно центра инверсии и антисимметричные относительно побочной оси вращения). Подробнее о символах Малликена см. по ссылке.
Энергия расщепления \(\Delta_o\)
Разница в энергии между вышележащими \(e_g\) и нижележащими \(t_{2g}\)-орбиталями — энергия расщепления — зависит от некоторых факторов, в первую очередь от:
- Электронного строения центрального атома (иона). d-Металлы и ионы d-металлов 4-го и 5-го периода имеют бо́льшую энергию расщепления, так как орбитали бо́льшего уровня обладают бо́льшей диффузностью и деформируемостью, что приводит к меньшему расстоянию до лигандов и, следовательно, бо́льшей энергией взаимодействия с ними. Итого, при движении вниз по Периодической таблице величина расщепления увеличивается.
- Степени окисления центрального иона. Бо́льший заряд на центральном ионе вызывает бо́льшее электростатическое взаимодействие лигандов с данным ионом и, соответственно, увеличивается энергию расщепления.
- Природы лиганда. В зависимости от того, какой лиганд образует комплекс с центральным атомом (ионом), достаточно сильно меняется энергия взаимодействия лигандов с данным атомом.
Фактор природы лигандов — главный фактор, влияющий на величину энергии расщепления. Однако, так как все лиганды в рамках теории кристаллического поля рассматриваются одинаково, ТКП не может указать причину такой зависимости величины расщепления от природы лиганда и эта причина рассматривается в рамках теории поля лигандов. Поэтому был эмпирически получен спектрохимический ряд лигандов, в котором перечислены некоторые лиганды слева направо по увеличению энергии расщепления кристаллическим полем:
При этом лиганды до \(\ce{H2O}\) называют лигандами слабого поля, а после \(\ce{H2O}\) — лигандами сильного поля, таким образом качественно указывая на величину энергии расщепления. Данная классификация лигандов необходима для определения магнитных свойств комплекса, о чём см. далее.
Низкоспиновые и высокоспиновые комплексы
При заполнении d-орбиталей (движении слева направо по периоду) электронами до конфигурации d3 включительно выполняется правило Хунда о достижении максимального спина, и электроны располагаются на \(t_{2g}\)-орбиталях:

Когда атом или ион имеет конфигурацию d4, становятся возможными два варианта заполнения электронами орбиталей. Если энергия расщепления \(\Delta_o\) небольшая, четвёртый электрон располагается на \(e_g\)-орбитали: приобретает бо́льшую энергию, в отличие от \(t_{2g}\)-электронов, однако при этом выполняется правило Хунда о достижении максимального суммарного спина:
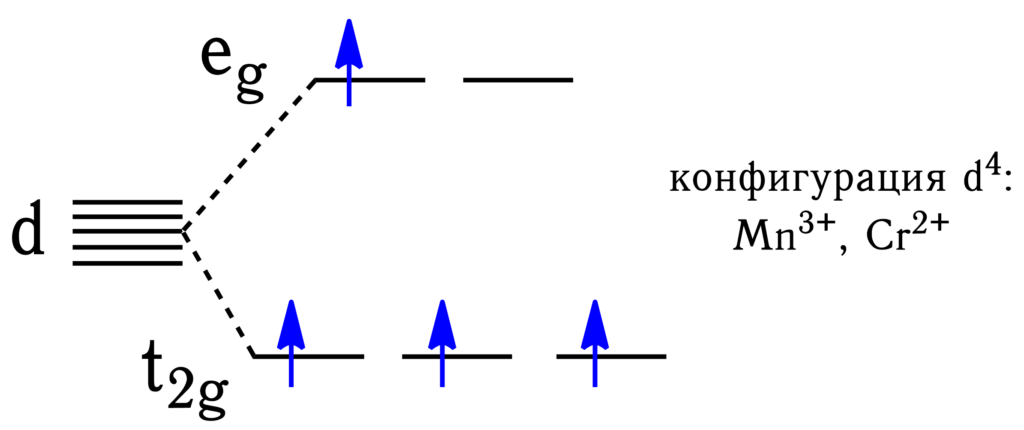
Такое состояние называют высокоспиновым, так как в данном случае выполняется правило Хунда и достигается максимальный (высокий) спин.
Если же величина энергии расщеплении достаточно большая, четвёртый электрон спаривается и располагается на \(t_{2g}\)-орбитали. При этом электрон должен преодолеть энергию спаривания, а значит: если энергия расщепления \(\Delta_o\) оказывается больше энергии спаривания \(P\), электрон спаривается и образуется низкоспиновое состояние атома или иона. При этом электрон выигрывает в энергии благодаря расположению на более низколежащей орбитали, и проигрывает за счёт преодоления энергии спаривания.

Например, в комплексном ионе \(\ce{[CoF6]^3-}\) энергия расщепления небольшая (так как \(\ce{F^-}\) — лиганд слабого поля), значит ион будет иметь высокоспиновую конфигурацию вследствие меньшей энергии расщепления по сравнению с энергией спаривания электронов. В свою очередь, ион \(\ce{[Co(NH3)6]^3+}\), за счёт наличия лиганда сильного поля \(\ce{NH3}\), обладает гораздо большей энергией расщепления, которая превышает энергию спаривания электронов, и комплекс становится низкоспиновым:
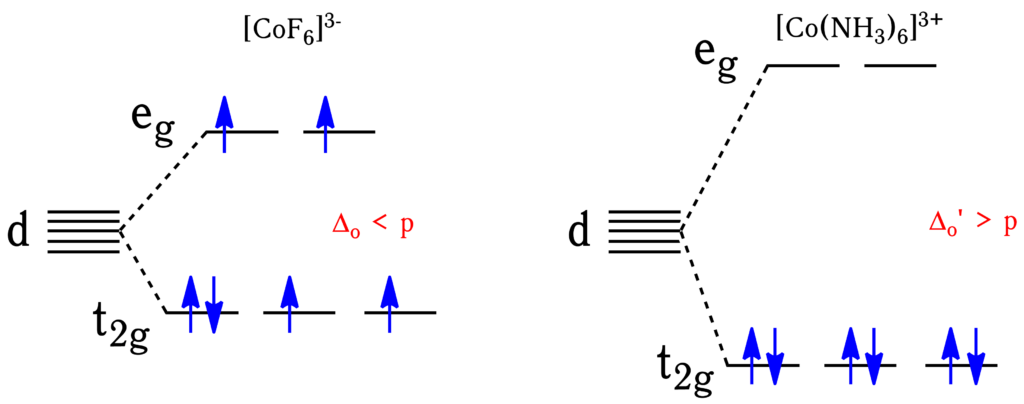
Магнитный момент
Магнитный момент комплексной частицы, вызванный наличием неспаренных электронов (для 3d металлов он близок к суммарному магнитному моменту), может быть вычислен по формуле: $$ \mu = \sqrt{n(n+2)},$$ где \(n\) — число неспаренных электронов. Он выражается в магнетонах Бора (мБ).
Например, для высокоспинового комплекса \(\ce{[CoF6]^3-}\), который имеет 4 неспаренных электрона, магнитный момент будет равен:
\(\mu = \sqrt{4(4+2)} = \sqrt{24} \approx 4,9\: mB\).
Энергия стабилизации кристаллическим полем
На рисунке ниже приведена зависимость энергии кристаллической решётки хлоридов \(\ce{MCl2}\) от количества d-электронов в металле M:

Видно, что график энергии решётки от количества d-электронов в металле имеет «холмы». Они вызваны дополнительной стабилизацией центрального иона: её обеспечивает так называемая энергия стабилизации кристаллическим полем (ЭСКП).
Её можно вычислить, умножив количество электронов на \(t_{2g}\)-орбитали на \(\frac{2}{5}\Delta_o\), и отняв от полученного количество электронов на \(e_g\)-орбитали, умноженное на \(\frac{3}{5}\Delta_o\).

Нетрудно догадаться, что в комплексе конфигурации d3 достигается максимальная ЭСКП, равная \(\frac{6}{5}\Delta_o\), что объясняет образование «холма» на графике зависимости энергии кристаллической решётки (выше).
При этом в случае образования низкоспинового комплекса со спариванием электронов при расчёте ЭСКП необходимо учитывать энергию спаривания (обычно обозначается буквой \(P\)).
ЭСКП в \(\ce{[CoF6]^3-}\) будет вычисляться по формуле: \(4*\frac{2}{5}\Delta_o — 2*\frac{3}{5}\Delta_o = \frac{2}{5}\Delta_o\), а в \(\ce{[Co(NH3)6]^3+}\) — по формуле \(6*\frac{2}{5}\Delta_o — 2P\), где \(P\) — энергия спаривания.
Эффект Яна-Теллера
Для комплексов с такими конфигурациями, когда имеет место орбитальное вырождение (в основном комплексы \(t_{2g}^3e_g^1\) и \(t_{2g}^6e_g^3\)), путём геометрического искажения и понижения симметрии происходит снятие вырождения и дополнительный выигрыш в энергии, который называется энергией стабилизации Яна-Теллера.
Подробнее про эффект Яна-Теллера см. статью по ссылке (статья в разработке).
Окраска комплексов
Из химии известно, что довольно много комплексных соединений d-металлов — окрашенные соединения, то есть они свободны поглощать энергию света в видимой области спектра. При этом поглощаются частицы света такой энергии, которая соответствует энергии расщепления кристаллическим полем:
$$\Delta_o = E_{light} = h\nu = h\frac{c}{\lambda}$$
При поглощении света определённой длины волны \(\lambda\) человеческий глаз видит дополнительный цвет. Дополнительные цвета (находятся напротив друг друга) достаточно наглядно отражены в колесе Ньютона:

Если вещество поглощает красный цвет (длина волны 630-700 нм), человеческий глаз видит зелёную окраску данного вещества.
Комплексы хрома(III): примеры
Хром в степени окисления +3 имеет довольно много разнообразных комплексов. Ион \(\ce{Cr^3+}\) имеет электронную конфигурацию \(d^3\), что обеспечивает максимальную ЭСКП, равную \(\frac{6}{5}\Delta_o\) в октаэдрическом поле.
На картинке ниже — примеры некоторых комплексов хрома(III): \(\ce{[Cr(H2O)4Cl2]^+, [Cr(H2O)6]^3+}\) (две по центру), \(\ce{[Cr(OH)6]^3-}\):

За счёт наличия разных лигандов, составляющих комплексную частицу, изменяется и параметр \(\Delta_o\), который напрямую влияет на цвет соединения. Наличие лигандов \(\ce{Cl^-}\) уменьшает \(\Delta_o\), так как является лигандом слабого поля, значит, увеличивает длину волны поглощаемого света и смещает её ближе к красной области длин волн. Дополнительный цвет для красного — зелёный, поэтому мы видим комплекс \(\ce{[Cr(H2O)4Cl2]^+}\) зелёным.
Аналогичная ситуация для остальных комплексов: вода является лигандом более сильного поля, значит, величина расщепления \(\Delta_o\) выше. Получается, что длина волны поглощаемого света меньше, что и обеспечивает такую окраску комплекса.
Тетраэдрическое окружение
При тетраэдрическом окружении картина расщепления выглядит противоположно октаэдрическому: выше по энергии располагаются орбитали \(t_2\)-симметрии, ниже — \(e\)-симметрии:

При этом величина энергии расщепления тетраэдрическим полем \(\Delta_t\) меньше величины расщепления октаэдрическим полем \(\Delta_o\), и связаны они при прочих равных соотношением:
\(\Delta_t = \frac{4}{9}\Delta_o\).
Расщепление в тетраэдрическом поле меньше, чем в октаэдрическом за счёт нескольких факторов, в первую очередь — меньшего количества окружающих лигандов, и таким расположением d-орбиталей, при котором энергия взаимодействия оказывается ниже.
Другие окружения
Ниже представлены орбитальные картины некоторых расщеплений:

Развитие теории
Теория кристаллического поля появилась как развитие простой модели электростатического взаимодействия между ионом (атомом) и лигандами и, как было упомянуто выше, не использует сведения о форме, природе и размере лигандов. Однако теория кристаллического поля по ходу истории своего становления была в дальнейшем объединена с методом молекулярных орбиталей (ММО) в общую теорию, позволяющую более подробно описывать свойства комплексных частиц — теорию поля лигандов. Читайте статью про теорию поля лигандов по ссылке. (статья в разработке).
